Pleaseomg

Learning Objectives

1. Explain the meaning of the equation of exchange, MV = PY, and tell why it must hold true.
2. Discuss the usefulness of the quantity theory of money in explaining the behavior of nominal GDP and inflation in the long run.
3. Discuss why the quantity theory of money is less useful in analyzing the short run.

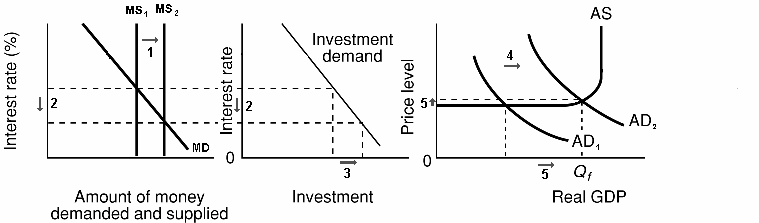
Real money demand is graphed holding fixed real income and expected inflation. The real money supply is equal to the nominal amount of M1, denoted M 0, divided by the fixed aggregate price level, P 0. It is assumed that the Fed does not alter the money supply based on the valued of the real interest rate.

So far we have focused on how monetary policy affects real GDP and the price level in the short run. That is, we have examined how it can be used—however imprecisely—to close recessionary or inflationary gaps and to stabilize the price level. In this section, we will explore the relationship between money and the economy in the context of an equation that relates the money supply directly to nominal GDP. As we shall see, it also identifies circumstances in which changes in the price level are directly related to changes in the money supply.

The Equation of Exchange

We can relate the money supply to the aggregate economy by using the equation of exchange:

Equation 11.1

The equation of exchange shows that the money supply M times its velocity V equals nominal GDP. Velocity is the number of times the money supply is spent to obtain the goods and services that make up GDP during a particular time period.

To see that nominal GDP is the price level multiplied by real GDP, recall from an earlier chapter that the implicit price deflator P equals nominal GDP divided by real GDP:

Equation 11.2

Multiplying both sides by real GDP, we have

Equation 11.3

Letting Y equal real GDP, we can rewrite the equation of exchange as

Equation 11.4

We shall use the equation of exchange to see how it represents spending in a hypothetical economy that consists of 50 people, each of whom has a car. Each person has $10 in cash and no other money. The money supply of this economy is thus $500. Now suppose that the sole economic activity in this economy is car washing. Each person in the economy washes one other person’s car once a month, and the price of a car wash is $10. In one month, then, a total of 50 car washes are produced at a price of $10 each. During that month, the money supply is spent once.

Applying the equation of exchange to this economy, we have a money supply M of $500 and a velocity V of 1. Because the only good or service produced is car washing, we can measure real GDP as the number of car washes. Thus Y equals 50 car washes. The price level P is the price of a car wash: $10. The equation of exchange for a period of 1 month is

[latex]$ 500 times 1 = $ 10 times 50[/latex]

Now suppose that in the second month everyone washes someone else’s car again. Over the full two-month period, the money supply has been spent twice—the velocity over a period of two months is 2. The total output in the economy is $1,000—100 car washes have been produced over a two-month period at a price of $10 each. Inserting these values into the equation of exchange, we have

[latex]$ 500 times 2 = $ 10 times 100[/latex]

Suppose this process continues for one more month. For the three-month period, the money supply of $500 has been spent three times, for a velocity of 3. We have

[latex]$ 500 times 3 = $ 10 times 150[/latex]

The essential thing to note about the equation of exchange is that it always holds. That should come as no surprise. The left side, MV, gives the money supply times the number of times that money is spent on goods and services during a period. It thus measures total spending. The right side is nominal GDP. But that is a measure of total spending on goods and services as well. Nominal GDP is the value of all final goods and services produced during a particular period. Those goods and services are either sold or added to inventory. If they are sold, then they must be part of total spending. If they are added to inventory, then some firm must have either purchased them or paid for their production; they thus represent a portion of total spending. In effect, the equation of exchange says simply that total spending on goods and services, measured as MV, equals total spending on goods and services, measured as PY (or nominal GDP). The equation of exchange is thus an identity, a mathematical expression that is true by definition.

To apply the equation of exchange to a real economy, we need measures of each of the variables in it. Three of these variables are readily available. The Department of Commerce reports the price level (that is, the implicit price deflator) and real GDP. The Federal Reserve Board reports M2, a measure of the money supply. For the second quarter of 2008, the values of these variables at an annual rate were

M = $7,635.4 billion

P = 1.22

Y = 11,727.4 billion

To solve for the velocity of money, V, we divide both sides of Equation 11.4 by M:

Equation 11.5

Using the data for the second quarter of 2008 to compute velocity, we find that V then was equal to 1.87. A velocity of 1.87 means that the money supply was spent 1.87 times in the purchase of goods and services in the second quarter of 2008.

Money, Nominal GDP, and Price-Level Changes

Assume for the moment that velocity is constant, expressed as V¯. Our equation of exchange is now written as

Equation 11.6

A constant value for velocity would have two important implications:

1. Nominal GDP could change only if there were a change in the money supply. Other kinds of changes, such as a change in government purchases or a change in investment, could have no effect on nominal GDP.
2. A change in the money supply would always change nominal GDP, and by an equal percentage.

In short, if velocity were constant, a course in macroeconomics would be quite simple. The quantity of money would determine nominal GDP; nothing else would matter.

Indeed, when we look at the behavior of economies over long periods of time, the prediction that the quantity of money determines nominal output holds rather well. Figure 11.6 “Inflation, M2 Growth, and GDP Growth” compares long-term averages in the growth rates of M2 and nominal GNP for 11 countries (Canada, Denmark, France, Italy, Japan, the Netherlands, Norway, Sweden, Switzerland, the United Kingdom, and the United States) for more than a century. These are the only countries that have consistent data for such a long period. The lines representing inflation, M2 growth, and nominal GDP growth do seem to move together most of the time, suggesting that velocity is constant when viewed over the long run.

Figure 11.6 Inflation, M2 Growth, and GDP Growth

The chart shows the behavior of price-level changes, the growth of M2, and the growth of nominal GDP for 11 countries using the average value of each variable. Viewed in this light, the relationship between money growth and nominal GDP seems quite strong.

Source: Alfred A. Haug and William G. Dewald, “Longer-Term Effects of Monetary Growth on Real and Nominal Variables, Major Industrial Countries, 1880–2001” (European Central Bank Working Paper Series No. 382, August 2004).

Moreover, price-level changes also follow the same pattern that changes in M2 and nominal GNP do. Why is this?

We can rewrite the equation of exchange, MV¯=PY in terms of percentage rates of change. When two products, such as MV¯ and PV, are equal, and the variables themselves are changing, then the sums of the percentage rates of change are approximately equal:

Equation 11.7

The Greek letter Δ (delta) means “change in.” Assume that velocity is constant in the long run, so that %ΔV = 0. We also assume that real GDP moves to its potential level, Y_P, in the long run. With these assumptions, we can rewrite Equation 11.7 as follows:

Equation 11.8

Subtracting %ΔY_P from both sides of Equation 11.8, we have the following:

Equation 11.9

Equation 11.9 has enormously important implications for monetary policy. It tells us that, in the long run, the rate of inflation, %ΔP, equals the difference between the rate of money growth and the rate of increase in potential output, %ΔY_P, given our assumption of constant velocity. Because potential output is likely to rise by at most a few percentage points per year, the rate of money growth will be close to the rate of inflation in the long run.

Several recent studies that looked at all the countries on which they could get data on inflation and money growth over long periods found a very high correlation between growth rates of the money supply and of the price level for countries with high inflation rates, but the relationship was much weaker for countries with inflation rates of less than 10%.^[1] These findings support the quantity theory of money, which holds that in the long run the price level moves in proportion with changes in the money supply, at least for high-inflation countries.

Why the Quantity Theory of Money Is Less Useful in Analyzing the Short Run

The stability of velocity in the long run underlies the close relationship we have seen between changes in the money supply and changes in the price level. But velocity is not stable in the short run; it varies significantly from one period to the next. Figure 11.7 “The Velocity of M2, 1970–2011” shows annual values of the velocity of M2 from 1960 to 2011. Velocity is quite variable, so other factors must affect economic activity. Any change in velocity implies a change in the demand for money. For analyzing the effects of monetary policy from one period to the next, we apply the framework that emphasizes the impact of changes in the money market on aggregate demand.

Figure 11.7 The Velocity of M2, 1970–2011

The annual velocity of M2 varied about an average of 1.78 between 1970 and 2011.

Source: Economic Report of the President, 2012, Tables B-1 and B-69.

The factors that cause velocity to fluctuate are those that influence the demand for money, such as the interest rate and expectations about bond prices and future price levels. We can gain some insight about the demand for money and its significance by rearranging terms in the equation of exchange so that we turn the equation of exchange into an equation for the demand for money. If we multiply both sides of Equation 11.1 by the reciprocal of velocity, 1/V, we have this equation for money demand:

Equation 11.10

The equation of exchange can thus be rewritten as an equation that expresses the demand for money as a percentage, given by 1/V, of nominal GDP. With a velocity of 1.87, for example, people wish to hold a quantity of money equal to 53.4% (1/1.87) of nominal GDP. Other things unchanged, an increase in money demand reduces velocity, and a decrease in money demand increases velocity.

If people wanted to hold a quantity of money equal to a larger percentage of nominal GDP, perhaps because interest rates were low, velocity would be a smaller number. Suppose, for example, that people held a quantity of money equal to 80% of nominal GDP. That would imply a velocity of 1.25. If people held a quantity of money equal to a smaller fraction of nominal GDP, perhaps owing to high interest rates, velocity would be a larger number. If people held a quantity of money equal to 25% of nominal GDP, for example, the velocity would be 4.

As another example, in the chapter on financial markets and the economy, we learned that money demand falls when people expect inflation to increase. In essence, they do not want to hold money that they believe will only lose value, so they turn it over faster, that is, velocity rises. Expectations of deflation lower the velocity of money, as people hold onto money because they expect it will rise in value.

In our first look at the equation of exchange, we noted some remarkable conclusions that would hold if velocity were constant: a given percentage change in the money supply M would produce an equal percentage change in nominal GDP, and no change in nominal GDP could occur without an equal percentage change in M. We have learned, however, that velocity varies in the short run. Thus, the conclusions that would apply if velocity were constant must be changed.

First, we do not expect a given percentage change in the money supply to produce an equal percentage change in nominal GDP. Suppose, for example, that the money supply increases by 10%. Interest rates drop, and the quantity of money demanded goes up. Velocity is likely to decline, though not by as large a percentage as the money supply increases. The result will be a reduction in the degree to which a given percentage increase in the money supply boosts nominal GDP.

Second, nominal GDP could change even when there is no change in the money supply. Suppose government purchases increase. Such an increase shifts the aggregate demand curve to the right, increasing real GDP and the price level. That effect would be impossible if velocity were constant. The fact that velocity varies, and varies positively with the interest rate, suggests that an increase in government purchases could boost aggregate demand and nominal GDP. To finance increased spending, the government borrows money by selling bonds. An increased supply of bonds lowers their price, and that means higher interest rates. The higher interest rates produce the increase in velocity that must occur if increased government purchases are to boost the price level and real GDP.

Just as we cannot assume that velocity is constant when we look at macroeconomic behavior period to period, neither can we assume that output is at potential. With both V and Y in the equation of exchange variable, in the short run, the impact of a change in the money supply on the price level depends on the degree to which velocity and real GDP change.

In the short run, it is not reasonable to assume that velocity and output are constants. Using the model in which interest rates and other factors affect the quantity of money demanded seems more fruitful for understanding the impact of monetary policy on economic activity in that period. However, the empirical evidence on the long-run relationship between changes in money supply and changes in the price level that we presented earlier gives us reason to pause. As Federal Reserve Governor from 1996 to 2002 Laurence H. Meyer put it: “I believe monitoring money growth has value, even for central banks that follow a disciplined strategy of adjusting their policy rate to ongoing economic developments. The value may be particularly important at the extremes: during periods of very high inflation, as in the late 1970s and early 1980s in the United States … and in deflationary episodes” (Meyer, 2001).

It would be a mistake to allow short-term fluctuations in velocity and output to lead policy makers to completely ignore the relationship between money and price level changes in the long run.

Key Takeaways

• The equation of exchange can be written MV = PY.
• When M, V, P, and Y are changing, then %ΔM + %ΔV = %ΔP + %ΔY, where Δ means “change in.”
• In the long run, V is constant, so %ΔV = 0. Furthermore, in the long run Y tends toward Y_P, so %ΔM = %ΔP.
• In the short run, V is not constant, so changes in the money supply can affect the level of income.

Try It!

The Case in Point on velocity in the Confederacy during the Civil War shows that, assuming real GDP in the South was constant, velocity rose. What happened to money demand? Why did it change?

Case in Point: Velocity and the Confederacy

The Union and the Confederacy financed their respective efforts during the Civil War largely through the issue of paper money. The Union roughly doubled its money supply through this process, and the Confederacy printed enough “Confederates” to increase the money supply in the South 20-fold from 1861 to 1865. That huge increase in the money supply boosted the price level in the Confederacy dramatically. It rose from an index of 100 in 1861 to 9,200 in 1865.

Estimates of real GDP in the South during the Civil War are unavailable, but it could hardly have increased very much. Although production undoubtedly rose early in the period, the South lost considerable capital and an appalling number of men killed in battle. Let us suppose that real GDP over the entire period remained constant. For the price level to rise 92-fold with a 20-fold increase in the money supply, there must have been a 4.6-fold increase in velocity. People in the South must have reduced their demand for Confederates.

An account of an exchange for eggs in 1864 from the diary of Mary Chestnut illustrates how eager people in the South were to part with their Confederate money. It also suggests that other commodities had assumed much greater relative value:

“She asked me 20 dollars for five dozen eggs and then said she would take it in “Confederate.” Then I would have given her 100 dollars as easily. But if she had taken my offer of yarn! I haggle in yarn for the millionth part of a thread! … When they ask for Confederate money, I never stop to chafer [bargain or argue]. I give them 20 or 50 dollars cheerfully for anything.”

Sources: C. Vann Woodward, ed., Mary Chestnut’s Civil War (New Haven, CT: Yale University Press, 1981), 749. Money and price data from E. M. Lerner, “Money, Prices, and Wages in the Confederacy, 1861–1865,” Journal of Political Economy 63 (February 1955): 20–40.

Answer to Try It! Problem

People in the South must have reduced their demand for money. The fall in money demand was probably due to the expectation that the price level would continue to rise. In periods of high inflation, people try to get rid of money quickly because it loses value rapidly.

References

Meyer, L. H., “Does Money Matter?” Federal Reserve Bank of St. Louis Review 83, no. 5 (September/October 2001): 1–15.

1. For example, one study examined data on 81 countries using inflation rates averaged for the period 1980 to 1993 (John R. Moroney, “Money Growth, Output Growth, and Inflation: Estimation of a Modern Quantity Theory,” Southern Economic Journal 69, no. 2 [2002]: 398–413) while another examined data on 160 countries over the period 1969–1999 (Paul De Grauwe and Magdalena Polan, “Is Inflation Always and Everywhere a Monetary Phenomenon?” Scandinavian Journal of Economics 107, no. 2 [2005]: 239–59). ↵

Last updated: February 2, 2000

Note: These notes are preliminary and incomplete and they are not guaranteed to be free of errors. Please let me know if you find typos or other errors.

The Asset Market

Up to now we have covered (1) the labor market and the production function, where real wages, employment and potential output is determined, and (2) the market for goods and services, where the real interest rate and investment and saving are determined. Now we consider the market for financial assets (money and 'bonds') by focusing on the demand and supply of money in the economy. This will give us insights into other forces on interest rates - particularly those created by the Fed - and also on the ultimate determinants of inflation.

What is Money?

• Medium of exchange - barter is inefficient.
• Unit of account - money is the basic unit for measuring economic value.
• Store of value - money can be used to hold wealth.
• Low return (interest rate) - money pays no interest
• Low risk - money is a 'safe' asset in low inflation times
• High liquidity - money is the most liquid asset (money is accepted immediately for almost all transactions)

Definitions of monetary aggregates

Symbol	Assets Included	Billions of dollars (1996)
C	Currency	$358.9
M1	Currency, demand deposits, traveler's checks, checkable deposits.	$1,095.3
M2	Currency, M1, overnight repos, eurodollars, money market deposit accounts, money market mutual funds, saving and small time deposits.	$3,761.1

In this class, when we talk about the nominal money supply we will generally be referring to the monetary aggregate M1. Hereafter, the symbol 'M' will denote M1.

The supply of money

The Federal Reserve Bank (Fed)

The Federal Reserve Bank (Fed) ultimately controls the supply of money in the economy. (How it does this and how the banking system works is detailed in the lectures on the Fed and Monetary Policy.) The Fed is the central bank for the U.S. and is a quasi-private entity (technically owned by private banks) created by the Federal Reserve Act in 1913. There are twelve regional Federal Reserve Banks across the country and the leadership of the system is conducted by the Board of Governors of the Federal Reserve System (Federal Reserve Board ). The Board consists of seven governors, appointed by the President to staggered fourteen-year terms. The President appoints one Board member as chairman - currently Allen Greenspan - for a term of four years. It is important to keep in mind that the Fed operates independently of the federal government. Congress and the President do not have direct control over the operations of the Fed.

How the Fed Controls the Money Supply

The Fed primarily controls the supply of money (M1) in the economy through what are called open market operations. These are the purchase and sale of government bonds by the Fed. The Fed operates the printing presses for the creation of currency. The Fed also owns a substantial amount of U.S. government bonds. When the Fed wants to increase the supply of money it performs an open market purchase of government bonds. That is, the Fed buys (by printing money) outstanding government bonds from the public or new government bonds from the Treasury (to finance the current deficit). This operations injects new cash into the economy. Conversely, when the Fed wants to decease the amount of money in the economy it performs an open market sale of government bonds. Here, the Fed sells some of its holdings of government bonds to the public in exchange for cash. This operation takes cash out of the economy.

Portfolio Allocation and the Demand for Assets

Portfolio theory tells us how individuals allocate their wealth among a number of financial assets (e.g. stocks, bonds, real estate, money). In general an individual's demand for assets is based on comparing the benefits of costs of holding different kinds of assets. These costs and benefits are functions of the following assets characteristics:

• Expected return - expected gain (or loss) from holding an asset over a particular investment horizon
• Risk - the degree of uncertainty in an asset's return
• Liquidity - the ease and quickness that an asset can be traded

An individual's demand for money is then based on the costs and benefits of holding money. As an asset, money has a very low expected return (it pays no interest), is very safe (the gov't guarantees its nominal value) and is the most liquid asset.

Simplifying assumptions

Since the general asset allocation problem involves many different kinds of assets with different risk and return characteristics we simplify this decision by assuming that there are only two kinds of financial assets in the economy.

• Money assets - low return, high liquidity and low risk. i_m = nominal interest rate on money assets (very low).
• Non-money assets (bonds) - higher return than on money assets and less liquidity. We assume that the risk associated with investing in bonds is not too high (think of government bonds as the generic non-money asset). Let i denote the nominal interest rate on non-money assets. Note that, by assumption, i > i_m. Also, recall that i = r +p^e, where r denotes the real return on non-money assets and p^e denotes expected inflation.

Behavorial Model for Money Demand

Our model for the demand for nominal money balances takes the following form

M^d = P·L^d(Y, i)

where

• M^d = demand for nominal money balances (demand for M1)
• L^d= demand for liquidity function
• P = aggregate price level (CPI or GDP deflator)
• Y = real income (real GDP)
• i = nominal interest rate on non-money assets

Discussion

• Nominal money demand is proportional to the price level. For example, if prices go up by 10% then individuals need 10% more money for transactions.
• As Y increases, desired consumption increases and so individuals need more money for the increased number of desired transactions. This is the liquidity demand for money.
• As the nominal interest rate on non-money assets (bonds), i, increases the opportunity cost of holding money increases and so the demand for nominal money balances decreases.
• Since i = r + p^e, we can decompose the effects on an increase in i into real interest rate increases (holding expected inflation fixed) and expected inflation increases (holding the real interest rate fixed).

The demand for real balances

Since the demand for nominal balances is proportional to the aggregate price level, we can divide both sides of the nominal money demand equation by P. This gives the liquidity demand function or the demand for real balances function:

MD = M^d/P = L^d(Y, i)

The left-hand-side of the above equation is the demand for nominal balances divided by the aggregate price level or the demand for real balances (the real purchasing power of money). The right-hand side is the liquidity demand function. The demand for real balances is decomposed into a transactions demand for money (captured by Y) and a portfolio demand for money (captured by i).

The real money demand function is graphed below:

How Does Supply Of Money Affect Equilibrium Real Gdp Percentage

Whenever income or expected inflation change the real money demand curves shifts. For example, if Y increases the real money demand function shifts up and right; if expected inflation increases the real money demand function shifts down and left.

Equilibrium in the money market

Real money demand and the real money supply as functions of the real interest rate are illustrated in the above graph. Real money demand is graphed holding fixed real income and expected inflation. The real money supply is equal to the nominal amount of M1, denoted M₀, divided by the fixed aggregate price level, P₀. It is assumed that the Fed does not alter the money supply based on the valued of the real interest rate. Therefore, the real money supply function is a vertical line in the graph with the real interest rate on the vertical axis and real money balances on the horizontal axis.

Notice that real money demand and real money supply intersect when the real interest rate is r₀. This is the value of the real interest that equates money demand with the money supply and establishes equilibrium in the money market. When the money market is in equilibrium there are no economic forces acting on the economy to alter the real interest rate.

If the real interest rate were r₁ then the demand for real balances would be greater than the fixed supply of real balances (as illustrated above). In this case we say there is an excess supply of money in the money market. Practically, what this means is that individuals are holding more money than they would like given the high real interest rate. Accordingly, individuals will attempt to rebalance their portfolios; i.e. they will try to get rid of money by buying bonds (our generic non-money asset). In doing so the demand for bonds increases and so the price of bonds increases. Because bond prices are inversely related to the interest rate on bonds, the increased price of bonds lowers the real return on bonds (holding expected inflation fixed). Therefore, the excess supply of money at r₁ (dis-equilibrium in the money market) leads to economic forces that act to lower the real interest rate. These forces cease to operate when the real interest falls to r₀ where the demand for real balances is equal to the supply of real balances.

Comparative statics

How Does Supply Of Money Affect Equilibrium Real Gdp Mean

Increase in the nominal money supply (M)

Consider the money market initially in equilibrium at r = 6% as illustrated in the above graph.. Suppose the Fed increases the nominal money supply by an open market purchase of government bonds. This increases the money supply from M₀ to M₁. Holding the price level fixed, this increases the supply of real balances from M₀/P₀to M₁/P₀. If the real interest rate stays at 6% then the supply of real balances will be greater than the demand for real balances: there will be an excess supply of money in the money market. Consequently, individuals will try to get rid of the excess money by buying bonds which puts downward pressure on the real interest rate (holding expected inflation fixed). As r drops we move along the liquidity demand curve toward the new equilibrium at r = 5%.

Increase in the aggregate price level (P)

Consider the money market initially in equilibrium at r = 6% described in the graph below. Now suppose that the aggregate price level increases from P₀ to P₁. Holding the nominal money supply fixed, this reduces the supply of real balances from M₀/P₀ to M₀/P₁. If the real interest rate stays at 6% the supply of real balances will be less than the demand for real balances: there will be an excess demand for money. The excess demand for money will prompt individuals to sell bonds (demand for bonds falls) and so the real interest rate on bonds will rise. As r rises, we move up along the liquidity demand curve toward the new equilibrium at r = 7%.

How Does Supply Of Money Affect Equilibrium Real Gdp Ratio

Consider the money market in equilibrium at r = 6% as illustrated above. Suppose that current income (Y), which is the same as current output (GDP),. Increases from Y₀ to Y₁. This increases the transactions demand for money as so the real money demand curve shifts up and to the right. If the real interest rate stays at 6% there will be an excess demand for money which puts upward pressure on the real interest rate. As r increases, we move along the money demand curve up towad the new equilibrium at r = 8%.